poniedziałek, 26 listopada 2012
poniedziałek, 19 listopada 2012
Procesy losowe - stochastyczne
Proces stochastyczny - rodzina zmiennych losowych określonych na pewnej przestrzeni probabilistycznej o wartościach w pewnej przestrzeni mierzalnej. Najprostszym przykładem procesu stochastycznego jest wielokrotny rzut monetą: dziedziną funkcji jest zbiór liczb naturalnych
(liczba rzutów), natomiast wartością funkcji dla danej liczby jest
jeden z dwóch możliwych stanów losowania (zdarzenie), orzeł lub reszka.
Nie należy mylić procesu losowego, którego wartości są zdarzeniami losowymi, z funkcją, która zdarzeniom przypisuje wartość prawdopodobieństwa ich wystąpienia (mamy wówczas do czynienia z rozkładem gęstości prawdopodobieństwa).
W praktyce dziedziną, na której zdefiniowana jest funkcja, jest najczęściej przedział czasowy (taki proces stochastyczny nazywany jest szeregiem czasowym) lub obszar przestrzeni (wtedy nazywany jest polem losowym). Jako przykłady szeregów czasowych można podać: fluktuacje giełdowe, sygnały, takie jak mowa, dźwięk i wideo, dane medyczne takie jak EKG i EEG, ciśnienie krwi i temperatura ciała, losowe ruchy takie jak ruchy Browna. Przykładami pól losowych są statyczne obrazy, losowe krajobrazy i układ składników w niejednorodnych materiałach.
 będzie niepustym zbiorem, który będziemy dalej nazywać zbiorem indeksów,
będzie niepustym zbiorem, który będziemy dalej nazywać zbiorem indeksów, 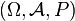 będzie przestrzenią probabilistyczną oraz
będzie przestrzenią probabilistyczną oraz  będzie przestrzenią mierzalną. Rodzinę zmiennych losowych
będzie przestrzenią mierzalną. Rodzinę zmiennych losowych
 -mierzalnych nazywamy procesem stochastycznym. Przestrzeń
-mierzalnych nazywamy procesem stochastycznym. Przestrzeń  nazywamy przestrzenią fazową albo przestrzenią stanów procesu
nazywamy przestrzenią fazową albo przestrzenią stanów procesu  .
.
Często za zbiór przyjmuje się przedział
przyjmuje się przedział 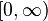 lub zbiór liczb naturalnych, za
lub zbiór liczb naturalnych, za  zbiór liczb rzeczywistych, a za
zbiór liczb rzeczywistych, a za  rodzinę
rodzinę  , to znaczy rodzinę borelowskich podzbiorów prostej.
, to znaczy rodzinę borelowskich podzbiorów prostej.
Procesy stochastyczne, których zbiór indeksów jest przeliczalny nazywamy łańcuchami.
W praktyce dziedziną, na której zdefiniowana jest funkcja, jest najczęściej przedział czasowy (taki proces stochastyczny nazywany jest szeregiem czasowym) lub obszar przestrzeni (wtedy nazywany jest polem losowym). Jako przykłady szeregów czasowych można podać: fluktuacje giełdowe, sygnały, takie jak mowa, dźwięk i wideo, dane medyczne takie jak EKG i EEG, ciśnienie krwi i temperatura ciała, losowe ruchy takie jak ruchy Browna. Przykładami pól losowych są statyczne obrazy, losowe krajobrazy i układ składników w niejednorodnych materiałach.
Definicja
Niech  będzie niepustym zbiorem, który będziemy dalej nazywać zbiorem indeksów,
będzie niepustym zbiorem, który będziemy dalej nazywać zbiorem indeksów, 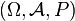 będzie przestrzenią probabilistyczną oraz
będzie przestrzenią probabilistyczną oraz  będzie przestrzenią mierzalną. Rodzinę zmiennych losowych
będzie przestrzenią mierzalną. Rodzinę zmiennych losowych ,
,
 -mierzalnych nazywamy procesem stochastycznym. Przestrzeń
-mierzalnych nazywamy procesem stochastycznym. Przestrzeń  nazywamy przestrzenią fazową albo przestrzenią stanów procesu
nazywamy przestrzenią fazową albo przestrzenią stanów procesu  .
.Często za zbiór
 przyjmuje się przedział
przyjmuje się przedział 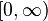 lub zbiór liczb naturalnych, za
lub zbiór liczb naturalnych, za  zbiór liczb rzeczywistych, a za
zbiór liczb rzeczywistych, a za  rodzinę
rodzinę  , to znaczy rodzinę borelowskich podzbiorów prostej.
, to znaczy rodzinę borelowskich podzbiorów prostej.Procesy stochastyczne, których zbiór indeksów jest przeliczalny nazywamy łańcuchami.
niedziela, 18 listopada 2012
Apoksymacja
Aproksymacja
jest dziełem analizy numerycznej zajmującym się najbardziej ogólnymi
zagadnieniami przybliżania funkcji, polegającymi na wyznaczaniu dla
danej funkcji f(x) takich funkcji F(x),które w określonym sensie
najlepiej przybliżają funkcję f(x).
Potrzeba przybliżenia danej funkcji inną funkcją pojawia się w wielu zadaniach. Może mieć np. zastosowanie przy obliczaniu funkcji standardowych lub wtedy, gdy funkcja f(x) jest zdefiniowana bardzo skomplikowanym wzorem. Jednym ze sposobów rozwiązania tego zadania jest przybliżanie funkcji f(x) sumami częściowymi ich rozwinięć w szeregi Taylora.
Zadania aproksymacyjne mogą być formułowane bardzo różnie, w zależności od przyjętego sposobu oszacowania błędów aproksymacji. Wyróżnia się trzy rodzaje aproksymacji:
aproksymację interpolacyjną
aproksymację jednostajną
aproksymację średniokwadratową

rysunek 5.6





Aproksymacja średniokwadratowa wielomianami








(5.67)





















Potrzeba przybliżenia danej funkcji inną funkcją pojawia się w wielu zadaniach. Może mieć np. zastosowanie przy obliczaniu funkcji standardowych lub wtedy, gdy funkcja f(x) jest zdefiniowana bardzo skomplikowanym wzorem. Jednym ze sposobów rozwiązania tego zadania jest przybliżanie funkcji f(x) sumami częściowymi ich rozwinięć w szeregi Taylora.
Zadania aproksymacyjne mogą być formułowane bardzo różnie, w zależności od przyjętego sposobu oszacowania błędów aproksymacji. Wyróżnia się trzy rodzaje aproksymacji:

rysunek 5.6
W przypadku aproksymacji
interpolacyjnej, podobnie jak w zagadnieniu interpolacji, żądamy
spełnienia warunku, aby funkcja dana f(x) i funkcja szukana F(x)
przyjmowały dokładnie te same wartości na zbiorze z góry ustalonych
punktów węzłowych. Warunek ten może być uzupełniony
warunkami wyrażającymi równość pochodnych w węzłach, jeżeli wartości
pochodnych zostaną zadane.


Twierdzenie
Weierstrassa gwarantuje że zawsze można znaleźć wielomian o dowolnie
małym odchyleniu od funkcji f(x) na przedziale [a,b]. Nie ma jednak
ogólnej metody umożliwiającej znajdowanie wielomianu najlepszego
przybliżenia jednostajnego stopnia n dla dowolnej funkcji ciągłej na
[a,b].
W przypadku aproksymacji średniokwadratowej jako miarę odchylenia funkcji od danej funkcji przyjmujemy wielkość
W przypadku aproksymacji średniokwadratowej jako miarę odchylenia funkcji od danej funkcji przyjmujemy wielkość

zwaną odchyleniem kwadratowym. Funkcja aproksymująca wyznaczana jest z
warunku, aby wartość wyrażenia była możliwie najmniejsza.
Geometrycznie warunek ten wyraża żądanie, aby pole powierzchni między
liniami reprezentującymi funkcję było minimalne.
Zagadnienia aproksymacji jednostajnej i aproksymacji średniokwadratowej są również formułowane dla funkcji określonych na dyskretnym zbiorze argumentów. Dla takich funkcji warunek (5.61) dotyczący aproksymacji jednostajnej zmienia się w ten sposób, że zamiast ciągłej zmiennej niezależnej x występuje w nim zmienna dyskretna Xi.
Zagadnienia aproksymacji jednostajnej i aproksymacji średniokwadratowej są również formułowane dla funkcji określonych na dyskretnym zbiorze argumentów. Dla takich funkcji warunek (5.61) dotyczący aproksymacji jednostajnej zmienia się w ten sposób, że zamiast ciągłej zmiennej niezależnej x występuje w nim zmienna dyskretna Xi.

a w rachunku na minimum odchylenia kwadratowego całka jest zastępowana sumą

Aproksymacja średniokwadratowa funkcji określonych na dyskretnym
zbiorze argumentów jest najczęściej wykorzystywana w zastosowaniach
praktycznych do wygładzania danych eksperymentalnych i wyników obliczeń
ze względu na mniej skomplikowane algorytmy jej realizacji numerycznej
w porównaniu z algorytmami aproksymacji jednostajnej i możliwość
uzyskiwania dobrych przybliżeń funkcji f(x). W niektórych przypadkach
istnieją przesłanki teoretyczne co do doboru postaci wzoru dla funkcji
aproksymującej ( wskazując dostatecznie wąską klasę funkcji np. zbiór
funkcji liniowych, potęgowych, wykładniczych itp. )- wtedy określamy
tylko wartości liczbowe parametrów, przy których przybliżenie danej
funkcji jest najlepsze.
Aproksymacja średniokwadratowa wielomianami
W zadaniach aproksymacji średniokwadratowej wielomianami funkcji
aproksymującej F(x) wygodnie jest poszukiwać w postaci wielomianu
uogólnionego

będącego kombinacją liniową liniowo-niezależnych funkcji.
Rozważając aproksymację średniokwadratową funkcji y=f(x) określonej na dyskretnym zbiorze argumentów współczynniki ai j=0,1...m funkcji (5.65) przyjmujemy tak , żeby funkcja

osiągnęła wartość minimalną. Zgodnie z ogólnymi metodami rachunku
różniczkowego funkcja osiąga minimum wtedy i tylko wtedy ,gdy znikają
pochodne cząstkowe względem wszystkich zmiennych a0,a1...ai :






Stąd otrzymujemy układ m+1 równań z m+1 niewiadomymi współczynnikami ,
z układem normalnym :
(5.67)




w którym wprowadzono skrócone oznaczenie

Układ równań ma dokładne jedno rozwiązanie dla liniowo - niezależnego układu funkcji:


Macierz współczynników jest macierzą symetryczną i dodatnio określoną.
Dla układu funkcji bazowych tworzących ciąg wielomianów

układ równań przyjmie postać:




gdzie:



Wielomian aproksymujący daną funkcję f(x) w sensie najmniejszych kwadratów

powinien mieć stopień na tyle wysoki, aby dostatecznie przybliżał
funkcję f(x), a jednocześnie mieć stopień wystarczająco niski, aby
wielomian ten wygładzał błędy losowe np. z pomiarów. Jeśli m=n, to
wielomian aproksymujący Qm(x) pokrywa się z wielomianem Lagrange'a dla układu punktów: x<0,x1, ... xm
i S=0 wtedy . Wiadomo, że dla m=>6 układ jest układem źle
uwarunkowanym, wskutek czego otrzymane wyniki mogą być bardzo zaburzone
i nie nadawać się do praktycznego wykorzystania. Podobnie więc jak w
przypadku interpolacji aproksymację średniokwadratową wielomianami
potęgowymi można zastosować tylko dla małych wartości m.
Trudności obliczeniowe związane z aproksymacją średniokwadratową za
pomocą wielomianów wyższych stopni mogą być zmniejszone przy
wykorzystaniu wielomianów ortogonalnych.
Średniokwadratowa aproksymacja trygonometryczna
W zagadnieniach , w których funkcja f(x) jest okresowa wygodnie jest
taką funkcję aproksymować nie wielomianami algebraicznymi, a
wielomianami trygonometrycznymi - tym bardziej, że ich odchylenia
kwadratowe od funkcji f(x) jest najmniejsze w porównaniu z odchyleniami
kwadratowymi dla innych wielomianów.
Jeżeli funkcja f(x) o okresie jest określona na dyskretnym zbiorze punktów i dane punkty są
równoległe, to korzystając z warunków ortogonalności zbioru funkcji:
jest określona na dyskretnym zbiorze punktów i dane punkty są
równoległe, to korzystając z warunków ortogonalności zbioru funkcji:
Jeżeli funkcja f(x) o okresie
 jest określona na dyskretnym zbiorze punktów i dane punkty są
równoległe, to korzystając z warunków ortogonalności zbioru funkcji:
jest określona na dyskretnym zbiorze punktów i dane punkty są
równoległe, to korzystając z warunków ortogonalności zbioru funkcji:



obliczamy współczynniki wielomianu trygonometrycznego

poniedziałek, 12 listopada 2012
Zmienne losowe - zadanie
Zadanie:
W wyniku długotrwałych obserwacji znana jest wariancja pomiarów pewnej wielkości,σ2 = 0,02. Ilu trzeba dokonać pomiarów tej wielkości, aby z prawdopodobieństwem średnia arytmetyczna otrzymanych wyników różniła się od wartości średniej o
średnia arytmetyczna otrzymanych wyników różniła się od wartości średniej o  ?
?
Rozwiązanie:
W wyniku długotrwałych obserwacji znana jest wariancja pomiarów pewnej wielkości,σ2 = 0,02. Ilu trzeba dokonać pomiarów tej wielkości, aby z prawdopodobieństwem
 średnia arytmetyczna otrzymanych wyników różniła się od wartości średniej o
średnia arytmetyczna otrzymanych wyników różniła się od wartości średniej o  ?
?Rozwiązanie:
 - pomocnicza zmienna losowa wyrażająca średnią arytmetyczną wyników pomiarów
- pomocnicza zmienna losowa wyrażająca średnią arytmetyczną wyników pomiarów
- mn = E(Mn) - wartość średnia wyników pomiarów
 - wariancja jednego pomiaru
- wariancja jednego pomiaru
- Z nierówności Czebyszewa wiemy, że:
- Obliczamy brakującą wariancję:
- Po podstawieniu do nierówności:
- Jako, że interesuje nas odwrona nierówność bierzemy dopełnienie prawdopodobieństwa:
- Z treści zadania wiemy, że dla
 :
:
- Po podstawieniu:
- Po podstawieniu reszty zmiennych i przekształceniach uzyskujemy:
- n = 200
- Z czego wynika, że trzeba dokonać co najmniej 200 pomiarów
Subskrybuj:
Posty (Atom)





