Metody Numeryczne: stycznia 2013

niedziela, 20 stycznia 2013

Testy

Źródło :
http://wazniak.mimuw.edu.pl/index.php?title=Rachunek_prawdopodobie%C5%84stwa_i_statystyka

niedziela, 13 stycznia 2013

Teoria prawdopodobieństwa – dział matematyki zajmujący się zdarzeniami losowymi. Rachunek prawdopodobieństwa zajmuje się badaniem abstrakcyjnych pojęć matematycznych stworzonych do opisu zjawisk, które nie są deterministyczne: zmiennych losowych w przypadku pojedynczych zdarzeń oraz procesów stochastycznych w przypadku zdarzeń powtarzających się (w czasie). Jako matematyczny fundament statystyki, teoria prawdopodobieństwa odgrywa istotną rolę w sytuacjach, w których konieczna jest analiza dużych zbiorów danych. Jednym z największych osiągnięć fizyki dwudziestego wieku było odkrycie probabilistycznej natury zjawisk fizycznych w skali mikroskopijnej, co zaowocowało powstaniem mechaniki kwantowej.
Matematyczna teoria prawdopodobieństwa sięga swoimi korzeniami do analizy gier losowych podjętej w siedemnastym wieku przez Pierre de Fermata oraz Blaise Pascala. Z tego powodu, początkowo teoria prawdopodobieństwa zajmowała się niemal wyłącznie zjawiskami dyskretnymi i używała metod kombinatorycznych. Zmienne ciągłe zostały wprowadzone do teorii prawdopodobieństwa znacznie później. Za początek stworzenia współczesnej teorii prawdopodobieństwa powszechnie uważa się jej aksjomatyzację, której w 1933 dokonał Andriej Kołmogorow. Współczesna teoria prawdopodobieństwa jest ściśle związana z teorią miary.
Pomimo że wynik pojedynczego rzutu monetą lub kością do gry często z praktycznego punktu widzenia można uważać za nieprzewidywalny, jeżeli eksperyment taki powtórzony zostaje wielokrotnie, mogą pojawić się pewne prawidłowości i wzory statystyczne, które można badać i przewidzieć. Dwa przykłady takich prawidłowości, i kluczowe osiągnięcia rachunku prawdopodobieństwa, to prawo wielkich liczb oraz centralne twierdzenie graniczne.

Definicja prawdopodobieństwa

Prawdopodobieństwem nazywamy dowolną funkcję $\, P$ o wartościach rzeczywistych, określoną na σ-ciele zdarzeń 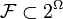$\mathcal{F} \subset 2^{\Omega}$ , spełniającą warunki:

(A1) $\, P(A) \ge 0$ dla każdego $\, A \in \mathcal{F}$ ;

(A2) $\, P(\Omega) = 1$ ;

(A3) Jeśli $\, A_n \in \mathcal{F},\; n\in\mathbb{N}$ oraz $A_i \cap A_j = \emptyset$ dla $\, i \neq j$ , to

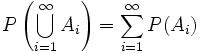
$\, P\left(\bigcup_{i=1}^{\infty}{A_i} \right) = \sum_{i=1}^{\infty}{P(A_i)}$ Warunki (A1-A3) zostały sformułowane przez Kołmogorowa w roku 1933 jako aksjomaty teorii prawdopodobieństwa.
Matematyczny model doświadczenia losowego to trójka
$\, (\Omega,\mathcal{F},P)$ gdzie $\, P$ jest prawdopodobieństwem, określonym na pewnym σ-ciele $\, \mathcal{F}$ podzbiorów zbioru zdarzeń elementarnych $\, \Omega$ . Trójkę tę nazywamy przestrzenią probabilistyczną

Wektory i wartości własne

Wektory i wartości własne – wielkości opisujące endomorfizm danej przestrzeni liniowej; wektor własny przekształcenia można rozumieć jako wektor, którego kierunek nie ulega zmianie po przyłożeniu do niego endomorfizmu; wartość własna odpowiadająca temu wektorowi to skala podobieństwa tych wektorów.
Najczęściej przekształcenie liniowe wyraża się jako macierz, która działa na wektory; wówczas stosuje się nazwy wektor własny macierzy, wartość własna macierzy. W innych teoriach przekształcenia i elementy przestrzeni liniowej mogą mieć inne nazwy. Mówi się wtedy przykładowo o stanach własnych operatora, funkcjach własnych funkcjonału itp.

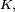Niech $\scriptstyle X$ będzie przestrzenią liniową nad ciałem $\scriptstyle K,$ zaś $\scriptstyle \mathrm T$ oznacza pewien jej endomorfizm, tzn. przekształcenie liniowe tej przestrzeni w siebie. Jeśli dla pewnego niezerowego wektora $\scriptstyle x$ przestrzeni spełniony jest warunek

$\mathrm Tx = \lambda x,$

gdzie $\scriptstyle \lambda$ jest pewnym skalarem, to $\scriptstyle x$ nazywa się wektorem własnym, a $\scriptstyle \lambda$ nazywa się wartością własną przekształcenia $\scriptstyle \mathrm T.$
Danej wartości własnej $\scriptstyle \lambda$ operatora $\scriptstyle \mathrm T$ odpowiada zbiór

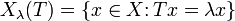
$X_\lambda(T) = \{x\in X\colon Tx = \lambda x\}$

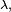nazywany podprzestrzenią własną odpowiadającą wartości własnej $\scriptstyle \lambda,$ gdyż tworzy on domkniętą podprzestrzenią liniową przestrzeni $\scriptstyle X.$ Jej wymiar nazywa się wielokrotnością wartości własnej $\lambda.$
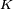Często zakłada się, że $\scriptstyle K$ jest ciałem liczb rzeczywistych bądź zespolona, zaś na $\scriptstyle X$ określona jest topologia liniowa. W zastosowaniach (np. równania różniczkowe) bada się często wartości własne operatorów liniowych określonych na przestrzeniach Banacha, Hilberta itp. W dalszej części artykułu będziemy zakładać ogólnie, że $\scriptstyle X$ jest pewną przestrzenią Banacha, a $\scriptstyle \mathrm T\colon X\to X$ jest ustalonym operatorem liniowym i ciągłym.